10th Maths Chapter 8 Statistics and Probability Exercise 8.5
1. Which of the following is not a measure of dispersion?
(1) Range
(2) Standard deviation
(3) Arithmetic mean
(4) Variance
Solution:
(3) Arithmetic mean
2.The range of the data 8, 8, 8, 8, 8. . . 8 is _____
(1) 0
(2) 1
(3) 8
(4) 3
Answer:
(1) 0
Hint:
Range = L – S = 8 – 8 = 0
3. The sum of all deviations of the data from its mean is
(1) Always positive
(2) always negative
(3) zero
(4) non-zero integer
Solution:
(3) zero
4. The mean of 100 observations is 40 and their standard deviation is 3. The sum of squares of all deviations is ______
(1) 40000
(2) 160900
(3) 160000
(4) 30000
Answer:
(2) 160900
Hint:

5. Variance of the first 20 natural numbers is
(1) 32.25
(2) 44.25
(3) 33.25
(4) 30
Solution:
(3) 33.25
6. The standard deviation of data is 3. If each value is multiplied by 5 then the new variance is ______
(1) 3
(2) 15
(3) 5
(4) 225
Answer:
(4) 225
Hint:
Standard deviation = 3
Each value is multiplied by 5
New standard deviation = 3 × 5 = 15
New variance = 152 = 225
7. If the standard deviation of x, y, z is p then the standard deviation of 3x + 5, 3y + 5, 3z + 5 is
(1) 3p + 5
(2) 3p
(3) p + 5
(4) 9p + 15
Solution:
(2) 3p
![]()
8. If the mean and coefficient of variation of a data are 4 and 87.5% then the standard deviation is _____
(1) 3.5
(2) 3
(3) 4.5
(4) 2.5
Answer:
(1) 3.5
Hint:
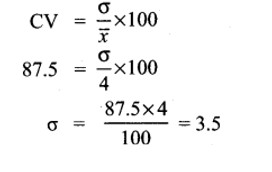
9. Which of the following is incorrect?
(1) P (A) > 1
(2) 0 ≤ P(A) ≤ 1
(3) P(ϕ) = 0 (4)
(4) P (A) + P(A¯¯¯¯) = 1
Solution:
(1) P(A) > 1
10.The probability a red marble selected at random from a jar containing p red, q blue and r green marbles is
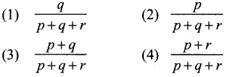
Solution:
(2) p/p+q+r
11.A page is selected at random from a book. The probability that the digit at units place of the page number chosen is less than 7 is

Solution:
(2) 7/10
12.The probability of getting a job for a person is x3. If the probability of not getting the job is 23 then the value of x is ____
(1) 2
(2) 1
(3) 3
(4) 1.5
Answer:
(2) 1
Hint:
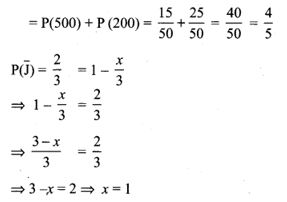
13. Kamalam went to play a lucky draw contest. 135 tickets of the lucky draw were sold. If the probability of Kamalam winning is 19, then the number of tickets bought by Kamalam is
(1) 5
(2) 10
(3) 15
(4) 20
Solution:
(3) 15
Hint:
=19×135=15
14.If a letter is chosen at random from the English alphabets {a, b, ……, z} then the probability that the letter chosen precedes x _______
(1) 12/13
(2) 1/13
(3) 23/26
(4) 3/26
Answer:
(3) 23/26
Hint:
![]()
15. A purse contains 10 notes of ₹ 2000, 15 notes of ₹ 500, and 25 notes of ₹ 200. One note is drawn at random. What is the probability that the note is either a ₹ 500 note or ₹ 200 note?
(1) 1/5
(2) 3/10
(3) 2/3
(4) 4/5
Solution:
(4) 4/5
CHAPTER 8
EX: 8 – STATISTICS AND PROBABILITY
![]()
1. The mean of the following frequency distribution is 62.8 and the sum of all frequencies is 50. Compute the missing frequencies f1 and f2.
Solution:
Mean \(\overline{x}\) = 62.8
\(\Sigma x\) = 50

2. The diameter of circles (in mm) drawn in a design are given below.
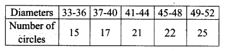
Claculate the standard deviation.
Solution:

3. The frequency distribution is given below.
![]()
In the table, k is a positive integer and has a variance of 160. Determine the value of k.
Solution:
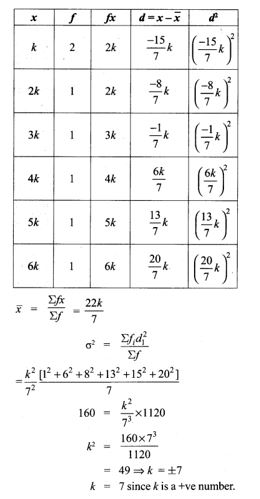
4. The standard deviation of some temperature data in degree Celsius (°C) is 5. If the data were converted into degree Fahrenheit (°F) then what is the variance?
Answer:
Standard deviation (σ) = 5
Variance = 52 = 25
We know the formula, F = \(\frac{9}{5}\) C + 32
Variance (F) = Vanance \(\frac{9}{5}\) C° + 32
[Variance of ax + b = a2 (variance of x)]
= \(\left(\frac{9}{5}\right)^{2}\) . variance
= \(\frac{81}{25}\) × 25
= 81° F
New variance = 81° F
![]()
5.If for a distribution, \(\Sigma(x-5)=3, \Sigma(x-5)^{2}=43\) and total number of observations is 18, find the mean and standard deviation.
Solution:

6. Prices of peanut packets in various places of two cities are given below. In which city, prices were more stable?

Solution:

7.If the range and coefficient of range of the data are 20 and 0.2 respectively, then find the largest and smallest values of the data.
Solution:
Range = L – S = 20

![]()
8.If two dice are rolled, then find the probability of getting the product of face value 6 or the difference of face values 5.
Solution:
Product of face values 6: {(1, 6), (2, 3), (6, 1), (3,2)}
Difference of face value 5: {(1, 6), (6, 1)}
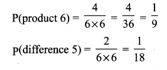
9. In a two children family, find the probability that there is at least one girl in a family.
Solution:
S = {BB, BG, GB, GG}
n(S) = 4
Event of atleast one girl in a family say A
A= {BG, GB, GG}
n( A) = 3
![]()
Probability of at least one girl in a family is \(\frac{3}{4}\)
10. A bag contains 5 white and some black balls. If the probability of drawing a black ball from the bag is twice the probability of drawing a white ball then find the number of black balls.
Solution:
Let a number of black balls be ‘x’.
Number of white balls = 5.

Number of Black balls = 10.
11. The probability that a student will pass the final examination in both English and Tamil is 0.5 and the probability of passing neither is 0.1. If the probability of passing the English examination is 0.75, what is the probability of passing the Tamil examination?
Solution:
P(English) = 0.75
P(Tamil) = x(assume)
P(English ∪ Tamil) = P(English) + P(Tamil) – P(English ∩ Tamil)
⇒ 1 – 0.1 = 0.75 + x – 0.5
⇒ x = 0.9 – 0.25
![]()
![]()
12. The King, Queen, and Jack of the suit spade are removed from a deck of 52 cards. One card is selected from the remaining cards. Find the probability of getting
(i) a diamond
(ii) a queen
(iii) a spade
(iv) a heart card bearing the number 5.
Solution:
King spade, Queen spade, Jack spade are removed
∴ total number of cards = 52 – 3 = 49.







