1. The curved surface area of a right circular cone of height 15 cm and base diameter 16 cm is ______
(1) 60π cm2
(2) 68π cm2
(3) 120π cm2
(4) 136π cm2
Answer:
(4) 136π cm2
Hint:

2. If two solid hemispheres of the same base radius r units are joined together along with their bases, then the curved surface area of this new solid is
(1) 4πr2 sq. units
(2) 67πr2 sq. units
(3) 3πr2 sq. units
(4) 8πr2 sq. units
Solution:
(1) 47πr2 sq. units]

3.The height of a right circular cone whose radius is 5 cm and slant height is 13 cm will be __________
(1) 12 cm
(2) 10 cm
(3) 13 cm
(4) 5 cm
Answer:
(1) 12 cm
Hint:

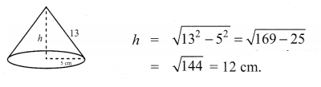
4. If the radius of the base of a right circular cylinder is halved keeping the same height, then the ratio of the volume of the cylinder thus obtained to the volume of original cylinder is
(1) 1 : 2
(2) 1 : 4
(3) 1 : 6
(4) 1 : 8
Solution:
(2) 1 : 4

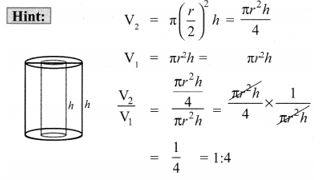
5. The total surface area of a cylinder whose radius is 13 of its height is

Solution:
(3) 8πh2/9 sq. units

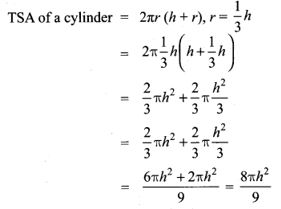
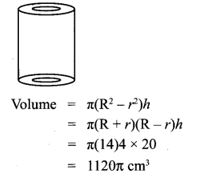
6. In a hollow cylinder, the sum of the external and internal radii is 14 cm and the width is 4 cm. If its height is 20 cm, the volume of the material in it is _______
(1) 560π cm3
(2) 1120π cm3
(3) 56π cm3
(4) 360π cm3
Answer:
(2) 1120π cm3
Hint:
R + r = 14 cm
w = 4 cm
h = 90 cm

7. If the radius of the base of a cone is tripled and the height is doubled then the volume is
(1) made 6 times
(2) made 18 times
(3) made 12 times
(4) unchanged
Solution:
(2) made 18 times
Hint:

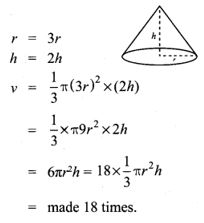
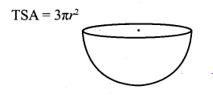
8. The total surface area of a hemisphere is how many times the square of its radius ______
(1) π
(2) 4π
(3) 3π
(4) 2π
Answer:
(3) 3π
Hint:

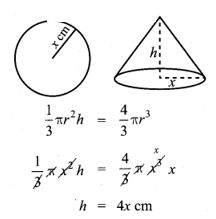
9. A solid sphere of radius x cm is melted and cast into a shape of a solid cone of the same radius. The height of the cone is
(1) 3x cm
(2) x cm
(3) 4x cm
(4) 2x cm
Solution:
(3) 4x cm
Hint:

10. A frustum of a right circular cone is of height 16 cm with radii of its ends as 8 cm and 20 cm. Then, the volume of the frustum is _______
(1) 3328π cm3
(2) 3228π cm3
(3) 3240π cm3
(4) 3340π cm3
Answer:
(1) 3328π cm3Hint:

11. A shuttlecock used for playing badminton has the shape of the combination of
(1) a cylinder and a sphere
(2) a hemisphere and a cone
(3) a sphere and a cone
(4) frustum of a cone and a hemisphere
Solution:
(4) frustum of a cone and a hemisphere

12. A spherical ball of radius r1 units is melted to make 8 new identical balls each of radius r2 units. Then r1 : r2 is
(1) 2 : 1
(2) 1 : 2
(3) 4 : 1
(4) 1 : 4
Solution:
Hint:

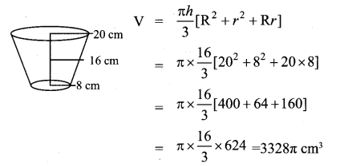
13. The volume (in cm3) of the greatest sphere that can be cut off from a cylindrical log of wood of base radius 1 cm and height 5 cm is

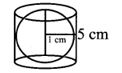
(1) 4/3π
(2) 10/3π
(3) 5π
(4) 20/3π

Solution:
(1) 4/3π

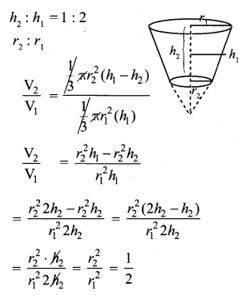
14. The height and radius of the cone of which the frustum is a part are h1 units and r1 units respectively. Height of the frustum is h2 units and the radius of the smaller base is r2 units. If h2: h1 = 1 : 2 then r2 : r1 is
(1) 1 : 3
(2) 1 : 2
(3) 2 : 1
(4) 3 : 1
Solution:
(2) 1 : 2

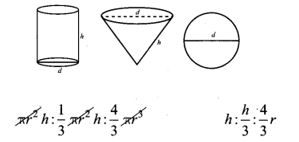
15. The ratio of the volumes of a cylinder, a cone and a sphere, if each has the same diameter and same height is ____
(1) 1 : 2 : 3
(2) 2 : 1 : 3
(3) 1 : 3 : 2
(4) 3 : 1 : 2
Answer:
(4) 3 : 1 : 2
Hint:

UNIT EXERCISE 7. MENSURATION

1. The barrel of a fountain-pen cylindrical in shape, is 7 cm long and 5 mm in diameter. A full barrel of ink in the pen will be used for writing 330 words on an average. How many words can be written using a bottle of ink containing one fifth of a litre?

Solution:

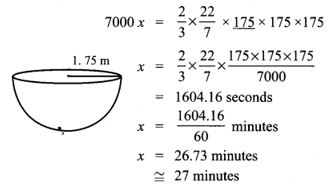
2. A hemi-spherical tank of radius 1.75 m is full of water. It is connected with a pipe which empties the tank at the rate of 7 litre per second. How much time will it take to empty the tank completely?

Solution:
Suppose the pipe takes x seconds to empty the tank. Then, volume of the water that flows out of the tank in x seconds = Volume of the hemispherical tank.
Volume of the water that flows out of the tank in x seconds.
= Volume of hemispherical shell of radius 175 cm.

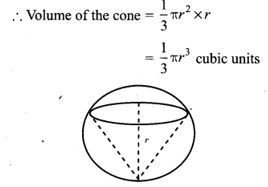
3. Find the maximum volume of a cone that can be carved out of a solid hemisphere of radius r units.

Solution:
Radius of the base of cone = Radius of the hemisphere = r
Height of the cone = Radius of the hemisphere

4. An oil funnel of tin sheet consists of a cylindrical portion 10 cm long attached to a frustum of a cone. If the total height is 22 cm, the diameter of the cylindrical portion be 8cm and the diameter of the top of the funnel be 18 cm, then find the area of the tin sheet required to make the funnel.

Solution:
Slant height of the frustum

5. Find the number of coins, 1.5 cm in diameter and 2 mm thick, to be melted to form a right circular cylinder of height 10 cm and diameter 4.5 cm.

Solution:
No. of coins required.

6. A hollow metallic cylinder whose external radius is 4.3 cm and internal radius is 1.1 cm

and whole length is 4 cm is melted and recast into a solid cylinder of 12 cm long. Find the diameter of solid cylinder.
Solution:
Volume of the solid cylinder = Volume of the hollow cylinder melted.

7. The slant height of a frustum of a cone is 4 m and the perimeter of circular ends are 18 m and 16 m. Find the cost of painting its curved surface area at ₹ 100 per sq. m.

Solution:

8. A hemi-spherical hollow bowl has material of volume 436π3 cubic cm. Its external diameter is 14 cm. Find its thickness.

Solution:

9. The volume of a cone is 100557 cu. cm. The area of its base is 20117 sq. cm. Find the slant height of the cone.

Solution:

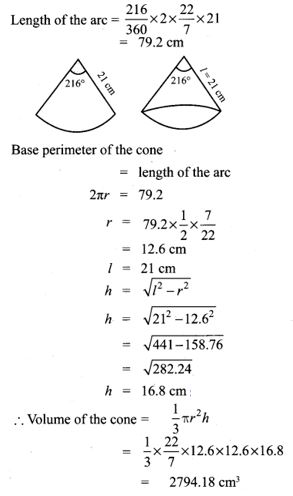
10. A metallic sheet in the form of a sector of T a circle of radius 21 cm has a central angle of 216°. The sector is made into a cone by bringing the bounding radii together. Find the volume of the cone formed.

Solution: