1. A 14 m deep well with an inner diameter 10 m is dug and the earth taken out is evenly spread all around the well to form an embankment of width of 5 m. Find the height of the embankment.

Solution:
Inner diameter = 10 m
Inner radius = 5 m
Inner height = 14 m

Volume of the cylinder = πr2h cubic units
=227×5×5×14
= 1100 m3
Volume of the hollow = n(R2 – r2)h cubic units
R = 10 m
r = 5 m
⇒227×(102−52)h=1100m3
(∵ the earth taken out = the earth spread all around)

2. A cylindrical glass with a diameter of 20 cm has water to a height of 9 cm. A small cylindrical metal of a radius of 5 cm and height of 4 cm is immersed it completely. Calculate the raise of the water in the glass?

Solution:
The volume of the water raised = the Volume of the cylindrical metal.

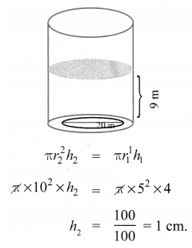
∴ The height of the raised water in the glass = 1 cm.

3. If the circumference of a conical wooden piece is 484 cm then find its volume when its height is 105 cm.

Solution:
Circumference of the base of the cone = 484 cm
height = 105 cm
∴ 2πr = 484

4. A conical container is fully filled with petrol. The radius is 10m and the height is 15 m. If the container can release the petrol through its bottom at the rate of 25 cu. meter per minute, in how many minutes the container will be emptied. Round off your answer to the nearest minute.

Solution:
Volume of the cone = 13πr2h cu. units.

5. A right-angled triangle whose sides are 6 cm, 8 cm, and 10 cm is revolved around the sides containing the right angle in two ways. Find the difference in volumes of the two solids so formed.

Solution:
When the triangle ABC is rotated about AB, the

6. The volumes of two cones of the same base radius are 3600 cm3 and 5040 cm3. Find the ratio of heights.

Solution:

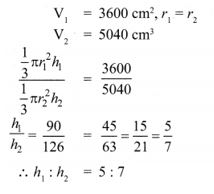
7. If the ratio of radii of two spheres is 4 : 7, find the ratio of their volumes.

Solution:

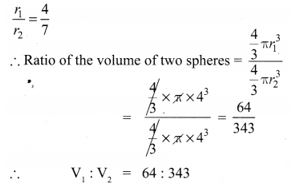
8. A solid sphere and a solid hemisphere have equal total surface area. Prove that the ratio of their volume is 3√3:4

Solution:

9. The outer and the inner surface areas of a spherical copper shell are 576π cm2 and 324π cm2 respectively. Find the volume of the material required to make the shell.

Solution:

10. A container open at the top is in the form of a frustum of a cone of height 16 cm with radii of its lower and upper ends are 8 cm and 20 cm respectively. Find the cost of milk which can completely fill a container at the rate of ₹ 40 per litre.

Solution:
The volume of the frustum