10th Standard Maths Chapter 2 Exercise 2.3 Numbers And Sequences Guide Book Back Answers Solutions. TN 10th SSLC Samacheer Kalvi Guide. 10th All Subject Guide – Click Here. Class 1 to 12 All Subject Book Back Answers – Click Here. 

• 10th Maths Chapter 2 Numbers And Sequences Full Answers Guide – Solutions 

1. Find the least positive value of x such that

• (i) 71 ≡ x (mod 8)
• (ii) 78 + x ≡ 3 (mod 5)
• (iii) 89 ≡ (x + 3) (mod 4)
• (iv) 96 = x7 (mod 5)
• (v) 5x ≡ 4 (mod 6)

Solution:
To find the least value of x such that
(i) 71 ≡ x (mod 8)
71 ≡ 7 (mod 8)
∴ x = 7.[ ∵ 71 – 7 = 64 which is divisible by 8]

(ii) 78 + x ≡ 3 (mod 5)
⇒ 78 + x – 3 = 5n for some integer n.
75 + x = 5 n
75 + x is a multiple of 5.
75 + 5 = 80. 80 is a multiple of 5.
Therefore, the least value of x must be 5.

(iii) 89 ≡ (x + 3) (mod 4)
89 – (x + 3) = 4n for some integer n.
86 – x = 4 n
86 – x is a multiple of 4.
∴ The least value of x must be 2 then
86 – 2 = 84.
84 is a multiple of 4.
∴ x value must be 2.

(iv) 96 ≡ x7 (mod 5)
96 – x7 = 5n for some integer n.
672−x7 = 5n
672 – x = 35n.
672 – x is a multiple of 35.
∴ The least value of x must be 7 i.e. 665 is a multiple of 35.

(v) 5x ≡ 4 (mod 6)
5x – 4 = 6M for some integer n.
5x = 6n + 4
x = 6n+45
When we put 1, 6, 11, … as n values in x = 6n+45 which is divisible by 5.
When n = 1, x = 105 = 2
When n = 6, x = 36+45 = 405 = 8 and so on.
∴ The solutions are 2, 8, 14…..
∴ Least value is 2.

2.If x is congruent to 13 modulo 17 then 7x – 3 is congruent to which number modulo 17?

Answer:
Given x ≡ 13 (mod 17) ……(1)
7x – 3 ≡ a (mod 17) ……..(2)
From (1) we get
x- 13 = 17 n (n may be any integer)
x – 13 is a multiple of 17
∴ The least value of x = 30
From (2) we get
7(30) – 3 ≡ a(mod 17)
210 – 3 ≡ a(mod 17)
207 ≡ a (mod 17)
207 ≡ 3(mod 17)
∴ The value of a = 3

3. Solve 5x ≡ 4 (mod 6)

Solution:
5x ≡ 4 (mod 6)
5x – 4 = 6M for some integer n.
5x = 6n + 4
x = 6n+45 where n = 1, 6, 11,…..
∴ x = 2, 8, 14,…

4. Solve 3x – 2 ≡ 0 (mod 11)

Solution:
3x – 2 ≡ 0 (mod 11)
3x – 2 = 11 n for some integer n.
3x = 11n + 2

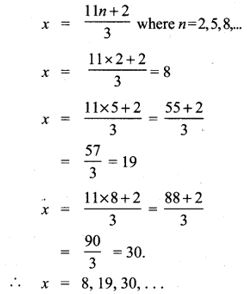
5. What is the time 100 hours after 7 a.m.?

Solution:
100 ≡ x (mod 12) (∵7 comes in every 12 hrs)
100 ≡ 4 (mod 12) (∵ Least value of x is 4)
∴ The time 100 hrs after 7 O’ clock is 7 + 4 = 11 O’ clock i.e. 11 a.m

6. What is time 15 hours before 11 p.m.?

Answer:
15 ≡ x (mod 12)
15 ≡ 3 (mod 12)
The value of x must be 3.

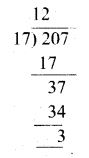
The time 15 hours before 11 o’clock is (11 – 3) 8 pm

7. Today is Tuesday. My uncle will come after 45 days. In which day my uncle will be coming?

Solution:
No. of days in a week = 7 days.
45 ≡ x (mod 7)
45 – x = 7n
45 – x is a multiple of 7.
∴ Value of x must be 3.
∴ Three days after Tuesday is Friday. Uncle will come on Friday.

8. Prove that 2n + 6 × 9n is always divisible by 7 for any positive integer n.

Answer:
9 = 2 (mod 7)
9n = 2n (mod 7) and 2n = 2n (mod 7)
2n + 6 × 9n = 2n (mod 7) + 6 [2n (mod 7)]
= 2n (mod 7) + 6 × 2n (mod 7)
7 × 2n (mod 7)
It is always divisible for any positive integer n

9. Find the remainder when 281 is divided by 17.

Solution:
281 ≡ x (mod 17)
240 × 240 × 241 ≡ x (mod 17)
(24)10 × (24)10 × 21 ≡ x (mod 17)
(16)10 × (16)10 × 2 ≡ x(mod 17)
(165)2 × (165)2 × 2
(165) ≡ 16 (mod 17)
(165)2 ≡ 162 (mod 17)
(165)2 ≡ 256 (mod 17)
≡ 1 (mod 17) [∵ 255 is divisible by 17]
(165)2 × (165)2 × 2 ≡ 1 × 1 × 2 (mod 17)
∴ 281 ≡ 2(mod 17)
∴ x = 2

10.The duration of flight travel from Chennai to London through British Airlines is approximately 11 hours. The aeroplane begins its journey on Sunday at 23:30 hours. If the time at Chennai is four and a half hours ahead to that of London’s time, then find the time in London, when will the flight lands at London Airport.

Solution:
The duration of the flight from Chennai to London is 11 hours.
Starting time at Chennai is 23.30 hrs. = 11.30 p.m.
Travelling time = 11.00 hrs. = 22.30 hrs = 10.30 a.m.
Chennai is 412 hrs ahead to London.
= 10.30 – 4.30 = 6.00
∴ At 6 a.m. on Monday the flight will reach at London Airport.